Storage Engines

Storage

Engines

The Simplest Database

Consider a simple database implemented as a key-value store. The underlying storage format is pretty simple - a text file where each line contains a key-value pair, separated by comma. Every write operation basically appends to the end of the file. So, if the same key is updated multiple times, the old versions of the key-value pairs are not overwritten - only the latest occurrence of the key is considered when reading the entry. This system has a pretty good performance since appending to a file is generally very efficient. Using similar concepts, many databases internally use a log, which is an append-only data file.

On the other hand, read operations on this system has terrible performance if there are a large number of records (key-value pairs) in the database. In algorithmic terms, the cost of a lookup is O(n).

Indexes

In order to efficiently find the value of a particular key in the database, a different data structure is used - index. An index is an additional structure that is derived from the primary data. Indexes do not affect the contents of a database, only the query performance.

While indexes increases performance on read queries, but it slows down write queries, because the index also needs to be updated every time data is written. This is an important trade-off in storage systems - well chosen indexes speed up read queries, but every index slows down writes.

For a key-value store, the simplest possible indexing strategy is - to keep an in-memory hash map where every key is mapped to a byte offset in the data file location at which the key-value pair can be found. When any new data is appended, the hash map is also updated to reflect the offset of that data. To lookup a value, use the hash map to find the offset in the data file, seek to that location and read the value.

Merging & Compaction

There is a possibility of eventually running out of disk space if data is continuously appended to the log. A good solution is to break the log file into segments of a certain pre-determined size by closing a segment file when it reaches a certain size, and making subsequent writes to a new segment file.

Then compaction can be performed on these segment files - throwing away duplicate keys in the log and keeping only the most recent update for each key. Moreover, since compaction usually makes segments much smaller, they can me merged at the same time as performing the compaction.

The merging and compaction of segments can be performed on a background thread, while it is going on, the database can continue to serve read queries on old segment files, and write queries on the latest segment file. After merging is complete, the database can now use the new merged segment file to handle read queries and the old segment files can be deleted.

Each segment file has its own in-memory hash map, mapping keys to the file offsets. During lookup the most recent segment file hash map is checked, then the second most recent and so on. The merging process keeps the number of segment files small, so lookups do not need to check many hash maps.

Disadvantages

The hash maps must fit in memory, because it is quite difficult to make hash maps on disk perform well. It requires a lot of random access I/O operations and is expensive to scale.
Range based queries are not efficient. Database still needs to lookup each key individually.

Edge Cases

Deleting Records - A special deletion record is appended to the data file (called tombstones). When log segments are merged, the records with deleted keys are ignored.
Recovery - If the database is restarted, the in-memory hash maps (indexes) are lost. Although the hash maps can be restored by reading entire segment files, it’s still very time consuming especially if the segment files are quite large. So instead, a snapshot of each segment file hash map is maintained on disk for faster recovery.
Concurrency Control - The simplest option is to have one writer thread. Since, the segments are append-only and immutable, multiple threads can read the data.

LSM Tree & SST Tables

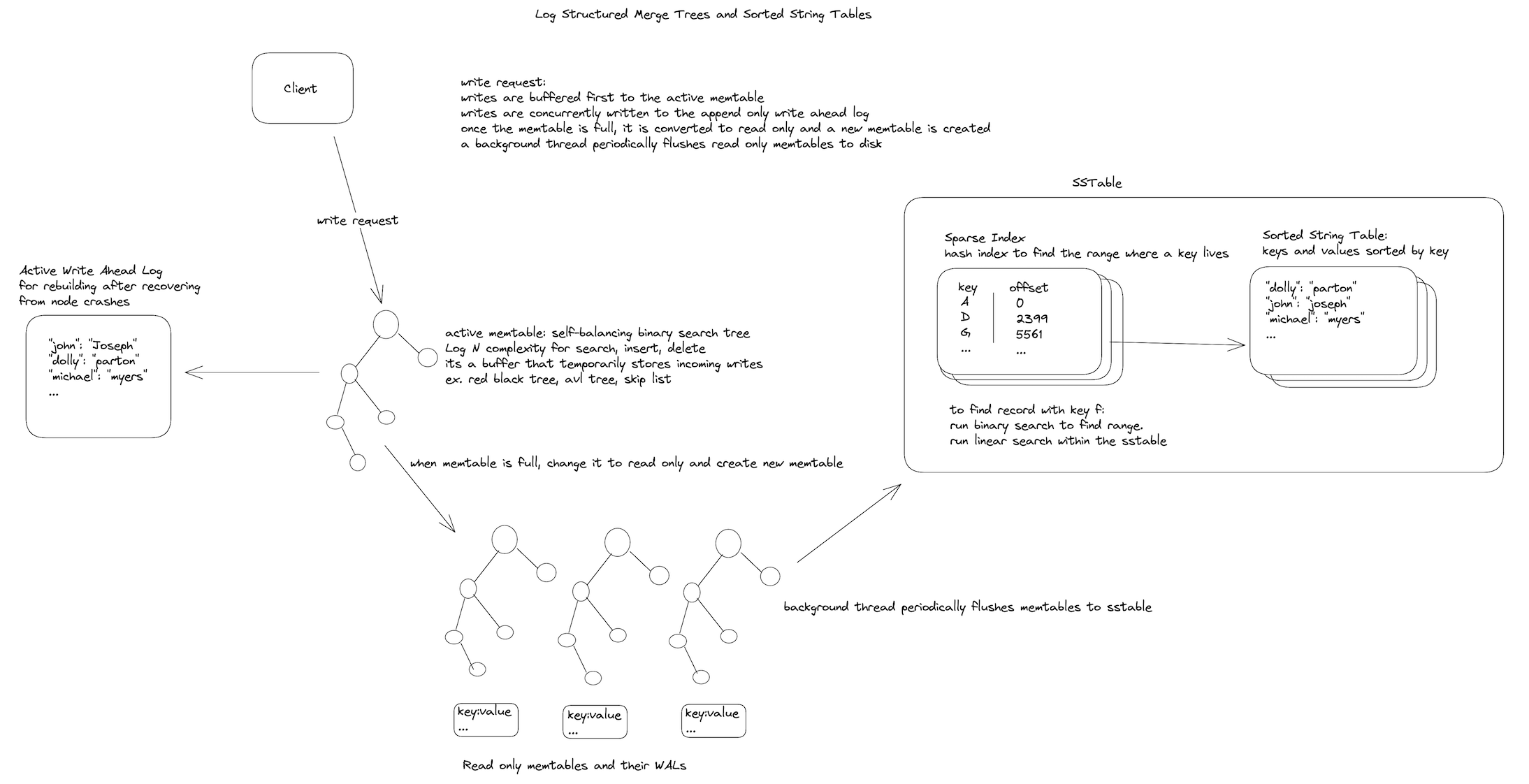
So, till now we understood that the log structured segment storage system is basically a sequence of key-value pairs. The values later in the log take precedence over the same key-values earlier since they appear in the order they are written.

One small modification is made to the segment files format - the sequence of the key-value pairs are sorted by key. This new format is called Sorted String Table or SSTable.

Advantages over Hash Indexes

Merging segment files is much more efficient. A similar approach to the merge sort algorithm is used.
In order to find a particular key, every single key does not need to be indexed. Keys can be indexed in sparse manner - maybe one key every few kilobytes of data.
The sparse key ranges can be further grouped and compressed into blocks before writing to disk. This will not only save disk space, but also reduce I/O bandwidth use.

Memtables

In order to maintain sorted data throughout the process, a balanced tree structure can be used like - AVL trees or Red-Black trees. Maintaining such a structure in-memory is much easier than it is on disk. This in-memory tree data structure is called memtable.

It seems that many modern databases implement the memtable as a skiplist, which although does not have deterministic balancing still is likely to be balanced due to the nature of its probabilistic insertions. It seems that a skip list may be preferable due to its comparatively simple implementation and concurrent access.

When the memtable gets bigger than a size threshold, the structure is flushed to disk as SST (Sorted String Table) file. While the SST table is being written out to disk, writes can continue on the memtable. It should be noted that in many implementations the memtable is flushed to disk in batches, and multiple memtables can be maintained for concurrent reads. Usually, only one memtable is available for writes and once full is turned immutable for reads only while a new memtable takes its place.

A read request can be served by first reading the memtable, then reading the latest SST table segment file and then the next latest SST table segment and so on. From time to time, a merge and compaction process is run to combine SST segments and discard duplicate (updated) keys or deleted keys.

This whole process is essentially what is used in LevelDB and RocksDB storage engines. Similar storage engines are used in CassandraDB & H-Base. Storage engines based on this principle are called LSM (Log-Structured Merge) Storage Engines and the indexing structure is often called Log-Structured Merge Tree (LSM Tree).

lsm-sst

Skiplists

Skip lists are a data structures that can be used instead of in-memory balanced trees. Skip lists use probabilistic balancing rather than strictly enforced balancing and as a result the algorithms for insertion and deletion in skip lists are much simpler and significantly faster than equivalent algorithms for balanced trees.

Skip lists are a probabilistic data structure that seem likely to supplant balanced trees as the implementation method of choice for many applications. Skip list algorithms have the same asymptotic expected time bounds as balanced trees and are simpler, faster and use less space.

~ William Pugh, Concurrent Maintenance of Skip Lists (1989)

Each element is represented by a node in a skip list. Each node has a height or level, which corresponds to the number of forward pointers the node has. A node’s ith forward pointer points to the next node of level i or higher. When a new element is inserted into the list, the level of the node is chosen randomly (for example, 50% are level 1, 25% are level 2, 12.5% are level 3 and so on.) without regard for the number of elements in the data structure.

A level i node has i forward pointers, indexed 1 through i. We do not need to store the level of a node in the node. Levels are capped at some appropriate constant MaxLevel. The level of a list is the maximum level currently in the list (or 1 if the list is empty). The header of a list has forward pointers at levels one through MaxLevel. The forward pointers of the header at levels higher than the current maximum level of the list point to NIL.

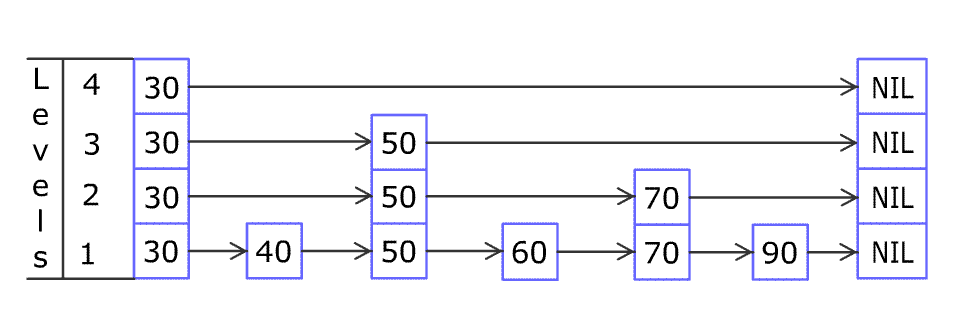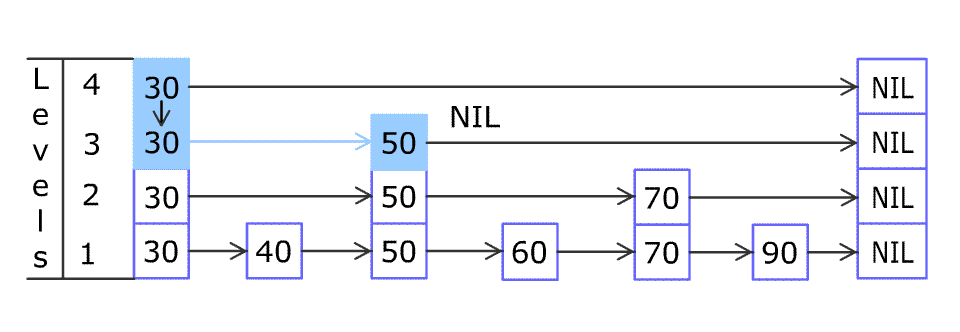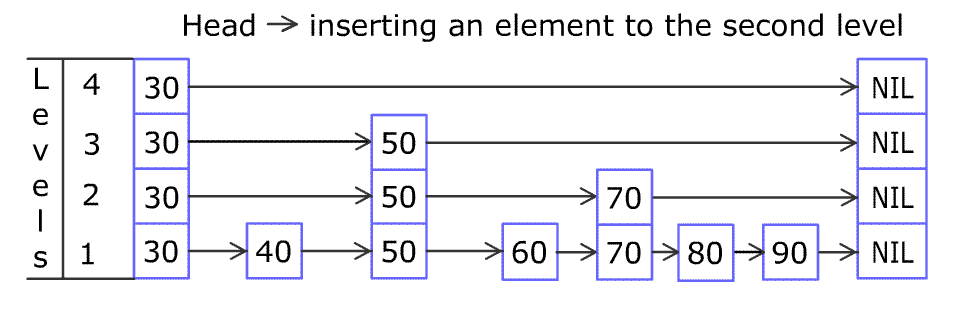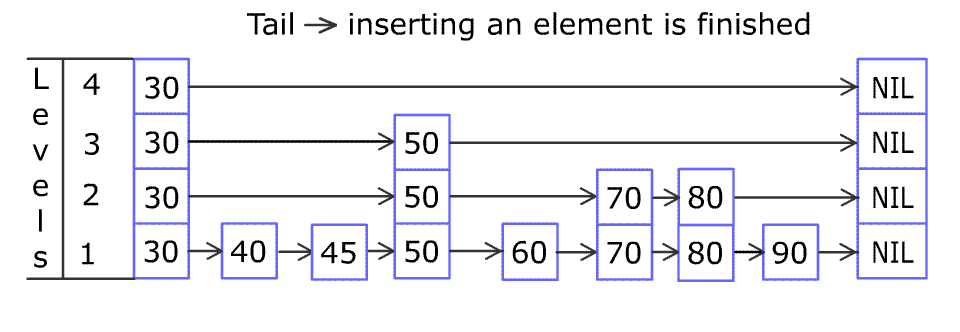
skiplists

Lookups work by traversing the node pointers starting from the highest level. If the search key is greater than the current node, the search continues forward on the same level. If the search key is lower than the current node, the search continues from the previous node's next lower level. During insertion, the insertion point is found using the same algorithm.

Apache Cassandra uses Skiplists for memtable implementation.

Bloom Filters

A Bloom Filter is a space efficient probabilistic data structure that can be used to test whether an element might be a member of a set or definitely not a member. The bloom filter will always say yes if an item is a set member. However, the bloom filter might still say yes although an item is not a member of the set (false positive).

Bloom Filter uses a large bit array (bit set) and multiple hash functions. The hash functions are applied to the keys of the records and based on the output from each hash function, the bit at the appropriate index in the bloom filter is set to 1.

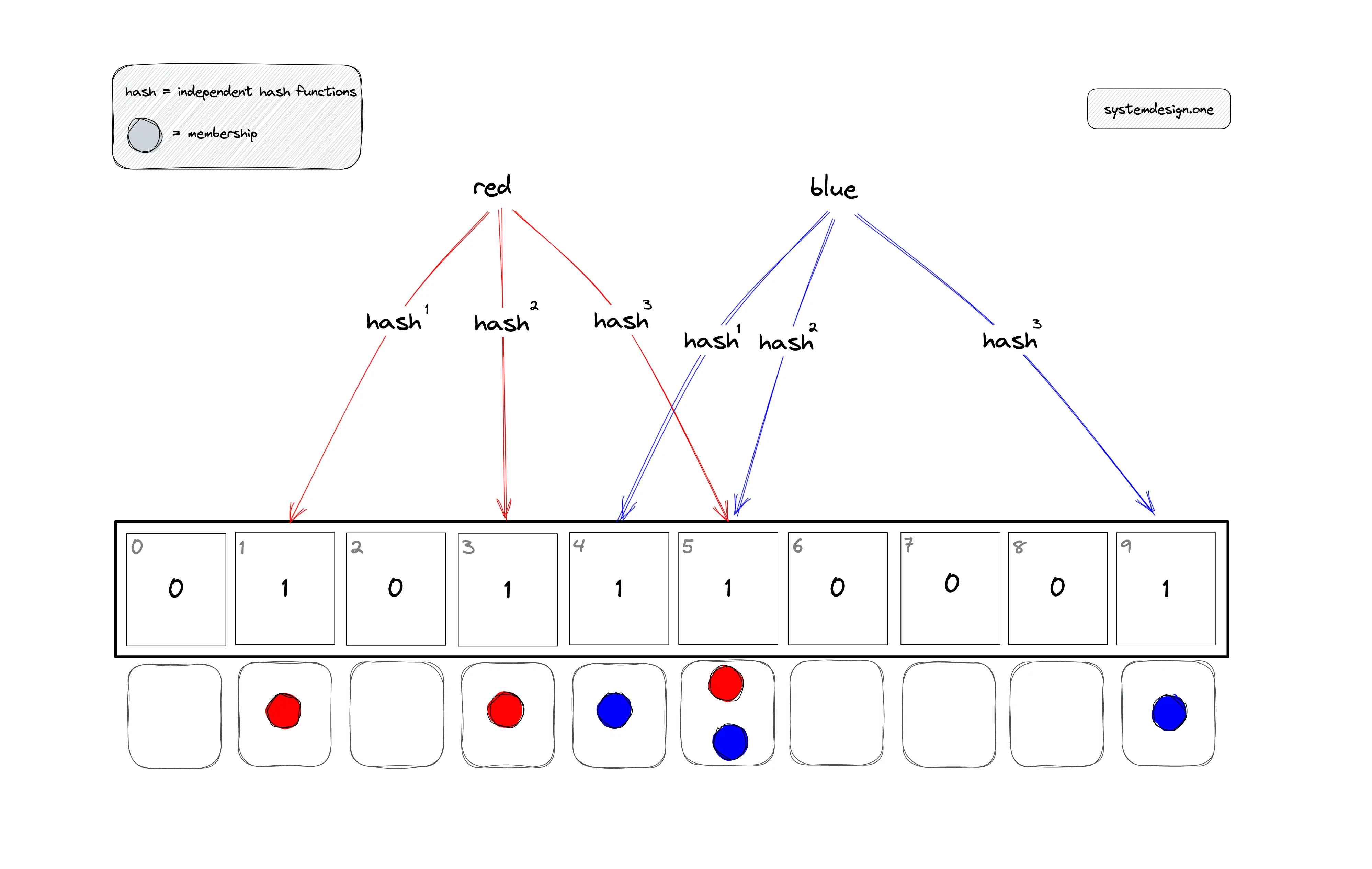
bloom-filter-update

During lookups, the hash functions are applied to the search key as well. If the bits determined by all the hash functions are 1, that means the key might be a member of the set. If at least one of the bits is 0, it means that the key is definitely not a member of the set.

Hash functions applied to different keys may return the same bit positions on the bloom filter, resulting in collisions. Probability of false positives is managed by configuring the size of the bit set and the number of hash functions. In a larger bit set there is a smaller chance of collisions. Similarly, having more hash functions also reduces the chances of collisions and false positives. However, using a larger bit set and having more hash functions results in more memory overhead and negative performance impact.

Implementations

B-Tree

Like SST tables, B-trees also keep data sorted by key, which makes for efficient lookups and ranged queries. However, unlike Log-structured indexes, the data is not broken down into segments. B-trees break down the database into fixed sized blocks or pages traditionally 4KB in size and read or write one page at a time by loading them into memory.

Each page can be referenced using an address on disk. So, a page can refer to another page using pointers. One page is designated as the “root” of the tree, where every single lookup is initiated from. Every page contains a continuous range of sorted keys and references to other “child” pages.

The number of references to child pages in one page if the B-tree is called the branching factor. The engine algorithm works like this —

For updating an existing key, the “leaf” page containing the corresponding key is searched. The key is updated and the page is then written to the disk.
For inserting a new key, the page with the proper key range is searched and the key is added in the page. If there is no more space, the page is broken down into two half-full pages, and the parent page is updated to account for the changes

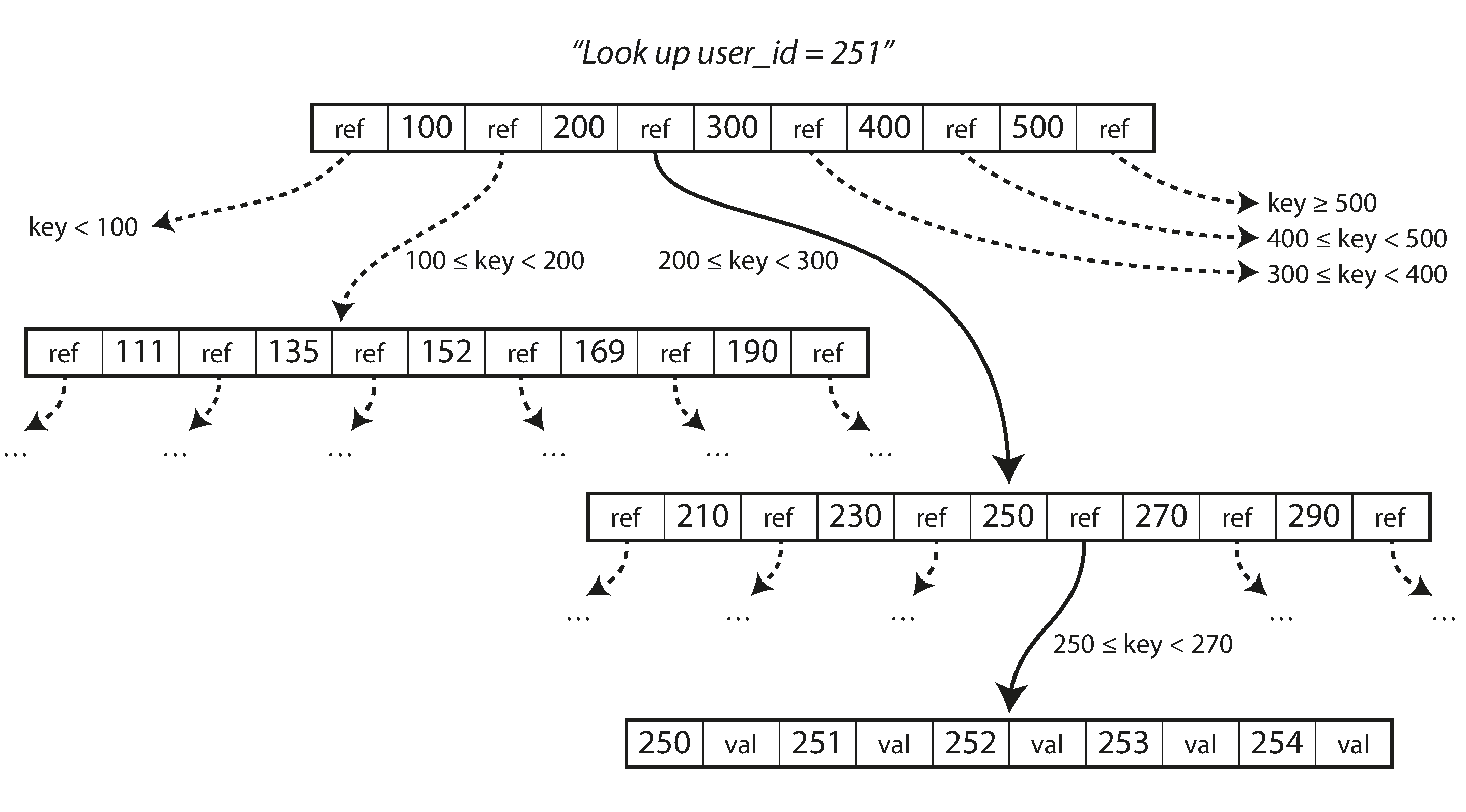
b-tree

This algorithm ensures that the tree remains balanced.

A B-tree with n keys always has a depth of O(log n). A four level tree of 4 KB pages with a branching factor of 500 can store up to 250 TB.

Write-Ahead Log

The basic write operation of a B-tree is to overwrite a page on disk with updated data. This is in contrast to indexes like LSM trees which only appends new data and never overwrites them. This is sometimes dangerous because if a write operation requires updation throughout multiple pages, and the database crashed midway, we end up with a corrupted index.

So, in order to make the database more resilient to crashes, an additional data structure is maintained on disk — called the write-ahead log (WAL, also known as redo log). This is an append-only file in which every B-tree modification must be written before they are actually carried out and applied on the pages itself.

This log is used to restore the state of the tree structure after a crash to a consistent state.

Concurrency Control

Careful concurrency control is required if multiple threads are going to access the B-tree at the same time — a thread may access inconsistent data otherwise. This is typically done by protecting the data structure using latches (lightweight locks).

Implementations

RUM Conjecture

One of the popular cost models for storage structures take three factors into consideration - Read, Update & Memory overheads. RUM conjecture states that reducing two of these overheads inevitably leads to change for the worse in the third one, and that optimisations can be done only at the expense of one of the three parameters.

B-Trees are read optmised. However, writes to the B-Tree require locating the appropriate page and record on the disk, and subsequent writes to the same page might have to update the page on disk multiple times. Furthermore, reserving extra space for future updates and deletions also increases memory overhead.

LSM trees do not require locating the records on the disk during writes and they do not reserve extra space for future writes or deletions either. Although there is some memory overhead resulting from sorting the redundant records. However, reads are generally more expensive because several different data structures and SST tables at different levels of compaction needs to checked depending on the record.

As a rule of thumb, LSM trees are typically faster for writes, whereas B-trees are faster for read operations. Reads are typically slower on LSM trees.

References

All Articles